Дифракція на воді

http://www.youtube.com/watch?feature=player_embedded&v=xh1_bzX1buA

Дифракція світла

Дифра́кція - явище, що виникає при поширенні хвиль (наприклад, світлових і звукових хвиль). Суть цього явища полягає в тому, що хвиля здатна огинати перешкоди. Це зумовлює те, що хвильовий рух спостерігається в області за перешкодою, куди хвиля не може потрапити прямо. Явище пояснюється інтерференцією хвиль на краях непрозорих об'єктів або неоднорідностях між різними середовищами на шляху поширення хвилі. Прикладом може бути виникнення кольорових світлових смуг в області тіні від краю непрозорого екрана.

Дифракція добре проявляється тоді, коли розмір перешкоди на шляху хвилі порівняний з її довжиною або менший.

Інтерференція світла від мильної плівки

http://www.youtube.com/watch?feature=player_embedded&v=wMPJ6KagJpo

Інтерференція світла

Інтерфере́нція (від лат. inter — взаємно, між собою; лат. ferio — вдаряю, вражаю) — явище накладання двох або більше когерентнихсвітлових хвиль в результаті чого в одних місцях спостерігається підсилення результуючої хвилі (інтерференційний максимум), а в інших місцях послаблення (інтерференційний мінімум).

Зони Френеля

Принцип Гюйгенса – Френеля

Принцип Гюйгенса – Френеля
Явище дифракції пояснюється за допомогою принципу Гюйгенса, згідно з яким кожна точка, до якої доходить хвиля, служить центром вторинних хвиль, а обвідна цих хвиль дає положення хвильового фронту в наступний момент часу.

Як приклад застосування принципу Гюйгенса розглянемо падіння плоскої хвилі на перешкоду з отвором (рис. 135). Коли хвильовий фронт доходить до перешкоди, то кожна точка отвору стає джерелом вторинних хвиль, а обвідна цих хвиль задає фронт хвилі, що пройшла через отвір. Цей фронт плоский лише в середній частині, а біля границі отвору відбувається загинання хвильового фронту, тобто хвиля проникає в область геометричної тіні, огинаючи краї перешкоди.



Принцип Гюйгенса – суто геометричний спосіб побудови хвильових поверхонь – розв’язує лише задачу про напрямок поширення хвильового фронту, але не зачіпає, по суті, питання про амплітуду, а отже, і про інтенсивність хвиль, що поширюються в різних напрямках. Френель вклав у принцип Гюйгенса фізичний зміст, доповнивши його ідеєю інтерференції вторинних хвиль. Принцип Гюйгенса – Френеля можна виразити такими положеннями:

1) під час розрахунку амплітуди світлових коливань, що збуджуються джерелом  в довільній точці М, джерело  можна замінити еквівалентною йому системою вторинних джерел – малих ділянок dS будь-якої замкненої допоміжної поверхні S, проведеної так, щоб вона охоплювала джерело  і не охоплювала розглядувану точку М;

2) вторинні джерела, які еквівалентні джерелу , когерентні між собою, тому вторинні хвилі, збуджені ними, інтерферують, і розрахунок інтерференції найбільш простий, якщо S – хвильова поверхня для світла джерела , оскільки при цьому фази коливань всіх вторинних джерел однакові;

3) амплітуда коливань, що збуджуються в точці М вторинним джерелом, пропорційна до площі dS відповідної ділянки хвильової поверхні, обернено пропорційна до відстані r від неї до точки М і залежить від кута  між зовнішньою нормаллю до хвильової поверхні і напрямком від елемента dS до точки М (рис. 136):

,

де  – фаза коливань в місці розміщення хвильової поверхні, a – величина, яка пропорційна до амплітуди первинних хвиль в точках елемента dS;  монотонно спадає від 1 при  до 0 при  (вторинні джерела не випромінюють назад); кут  називається кутом дифракції.



Урахування амплітуд і фаз вторинних хвиль дозволяє в кожному конкретному випадку знайти амплітуду результуючої хвилі в довільній точці простору, тобто визначити закономірності поширення світла.

Результуюче коливання в точці М являє собою суперпозицію коливань , взятих для всієї хвильової поверхні S:

.

Ця формула є аналітичним виразом принципу Гюйгенса – Френеля.

принцип Гюйгенса френеля

Цікаво знати про кільця Ньютона

Кільця Ньютона

Візьмемо плоску скляну пластинку і покладемо на неї плоско-опуклу лінзу великого радіуса кривизни (мал. 4.50).



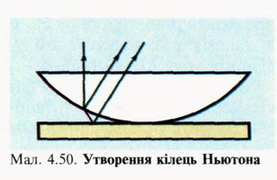
Спрямуємо на лінзу широкий пучок світла. Навколо точки стикання лінзи і пластинки побачимо концентричні світлі і темні кільця (мал. 4.51).



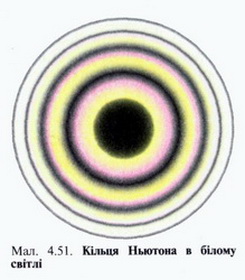
У фізиці їх називають кільцями Ньютона, на честь ученого, який вперше спостерігав і описав їх.

Кільця Ньютона — інтерференційний ефект

Картина, що спостерігається, є проявом явища інтерференції в системі лінза—пластинка (див. мал. 4.50). Якщо пучок світла падає на плоску поверхню лінзи, то він частково проходить крізь неї, відбивається від нижньої поверхні лінзи та поверхні скляної пластинки. Внаслідок цього утворюються два когерентні пучки, які утворюють стійку інтерференційну картину. Якщо пучок широкий і охоплює всю плоску поверхню лінзи, то в ній спостерігатимуться темні і світлі концентричні кільця. Пригадавши умови утворення інтерференційної картини, можна дійти висновку, що темні смуги охоплюють усі точки простору між лінзою і пластинкою, в яких різниця ходу між відбитими пучками дорівнює непарній кількості півхвиль:



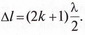
Відповідно для світлих смуг різниця ходу відбитих пучків дорівнює парній кількості півхвиль:



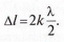
Радіуси кілець Ньютона для хвиль різної довжини будуть різними. Це добре видно з мал. 4.52, де наведено фотографії кілець для зеленого і червоного світла. Знаючи радіус кривизни лінзи, за розмірами кілець Ньютона можна визначити довжину хвилі падаючого світла.



Кільця Ньютона спостерігатимугься і тоді, коли світло проходить крізь лінзу і пластинку. Проте в цьому разі темні і світлі кільця поміняються місцями.

Ідею кілець Ньютона застосовують для високоточного контролю якості оброблюваних поверхонь. Для цього на контрольовану поверхню кладуть плоску пластинку, якість якої відома. Якщо пластинку освітлювати монохроматичним світлом, то в тих місцях, де поверхні не стикаються, з'являться інтерференційні смуги, форма яких відповідатиме формі нерівностей досліджуваної поверхні. Розміри цих нерівностей можна визначити з точністю до півдовжини хвилі використаного світла.