Кільця Ньютона
Візьмемо плоску скляну пластинку і покладемо на неї плоско-опуклу лінзу великого радіуса кривизни (мал. 4.50).
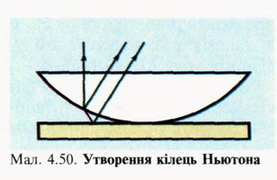
Спрямуємо на лінзу широкий пучок світла. Навколо точки стикання лінзи і пластинки побачимо концентричні світлі і темні кільця (мал. 4.51).
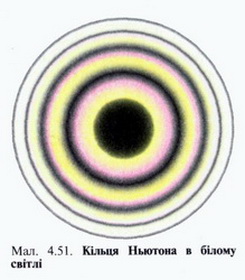
У фізиці їх називають кільцями Ньютона, на честь ученого, який вперше спостерігав і описав їх.
Кільця Ньютона — інтерференційний ефект
Картина, що спостерігається, є проявом явища інтерференції в системі лінза—пластинка (див. мал. 4.50). Якщо пучок світла падає на плоску поверхню лінзи, то він частково проходить крізь неї, відбивається від нижньої поверхні лінзи та поверхні скляної пластинки. Внаслідок цього утворюються два когерентні пучки, які утворюють стійку інтерференційну картину. Якщо пучок широкий і охоплює всю плоску поверхню лінзи, то в ній спостерігатимуться темні і світлі концентричні кільця. Пригадавши умови утворення інтерференційної картини, можна дійти висновку, що темні смуги охоплюють усі точки простору між лінзою і пластинкою, в яких різниця ходу між відбитими пучками дорівнює непарній кількості півхвиль:
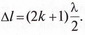
Відповідно для світлих смуг різниця ходу відбитих пучків дорівнює парній кількості півхвиль:
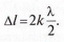
Радіуси кілець Ньютона для хвиль різної довжини будуть різними. Це добре видно з мал. 4.52, де наведено фотографії кілець для зеленого і червоного світла. Знаючи радіус кривизни лінзи, за розмірами кілець Ньютона можна визначити довжину хвилі падаючого світла.

Кільця Ньютона спостерігатимугься і тоді, коли світло проходить крізь лінзу і пластинку. Проте в цьому разі темні і світлі кільця поміняються місцями.
Ідею кілець Ньютона застосовують для високоточного контролю якості оброблюваних поверхонь. Для цього на контрольовану поверхню кладуть плоску пластинку, якість якої відома. Якщо пластинку освітлювати монохроматичним світлом, то в тих місцях, де поверхні не стикаються, з'являться інтерференційні смуги, форма яких відповідатиме формі нерівностей досліджуваної поверхні. Розміри цих нерівностей можна визначити з точністю до півдовжини хвилі використаного світла.
Візьмемо плоску скляну пластинку і покладемо на неї плоско-опуклу лінзу великого радіуса кривизни (мал. 4.50).

Спрямуємо на лінзу широкий пучок світла. Навколо точки стикання лінзи і пластинки побачимо концентричні світлі і темні кільця (мал. 4.51).

У фізиці їх називають кільцями Ньютона, на честь ученого, який вперше спостерігав і описав їх.
Кільця Ньютона — інтерференційний ефект
Картина, що спостерігається, є проявом явища інтерференції в системі лінза—пластинка (див. мал. 4.50). Якщо пучок світла падає на плоску поверхню лінзи, то він частково проходить крізь неї, відбивається від нижньої поверхні лінзи та поверхні скляної пластинки. Внаслідок цього утворюються два когерентні пучки, які утворюють стійку інтерференційну картину. Якщо пучок широкий і охоплює всю плоску поверхню лінзи, то в ній спостерігатимуться темні і світлі концентричні кільця. Пригадавши умови утворення інтерференційної картини, можна дійти висновку, що темні смуги охоплюють усі точки простору між лінзою і пластинкою, в яких різниця ходу між відбитими пучками дорівнює непарній кількості півхвиль:
Відповідно для світлих смуг різниця ходу відбитих пучків дорівнює парній кількості півхвиль:
Радіуси кілець Ньютона для хвиль різної довжини будуть різними. Це добре видно з мал. 4.52, де наведено фотографії кілець для зеленого і червоного світла. Знаючи радіус кривизни лінзи, за розмірами кілець Ньютона можна визначити довжину хвилі падаючого світла.

Кільця Ньютона спостерігатимугься і тоді, коли світло проходить крізь лінзу і пластинку. Проте в цьому разі темні і світлі кільця поміняються місцями.
Ідею кілець Ньютона застосовують для високоточного контролю якості оброблюваних поверхонь. Для цього на контрольовану поверхню кладуть плоску пластинку, якість якої відома. Якщо пластинку освітлювати монохроматичним світлом, то в тих місцях, де поверхні не стикаються, з'являться інтерференційні смуги, форма яких відповідатиме формі нерівностей досліджуваної поверхні. Розміри цих нерівностей можна визначити з точністю до півдовжини хвилі використаного світла.
Немає коментарів:
Дописати коментар